Optimal Deep Learning of Holomorphic Operators between Banach Spaces

Venue

NeurIPS

Year

2024

Authors

Ben Adcock, Nick Dexter, Sebastian Moraga

Topic

ML Theory

🌟 Highlights

• This was fairly dense, and honestly a bit challenging to read as it's a bit outside my comfort zone mathematically. Nonetheless, after some time, I think I have a good idea what's going on, and learned quite a bit afer I obtained a surface level picture.

• The core problem that this paper is trying to solve is establishing optimal generalization bounds for learning operator $F : X \rightarrow Y$ where both X and Y are (possibly infinite-dimensional) Banach Spaces. Put more concretely, the DNN learns an approximation of the solution map to a parametric PDE. This paper approaches the problem by using deep neural networks (DNNs) to approximate F and attempts to establish theoretical guarantees around using DNNs for this application.

📝 Summary

Operator learning, or learning operators that map between function spaces, arise for a variety of problems in computational science and engineering. Both Hilbert, and the more general Banach spaces are typically used as the input and output solution spaces and posed in terms of Partial Differential Equations (PDEs). The authors offers a rigorous a theoretical analysis of using Deep Neural Networks for learning non-linear holomorphic operators over Banach spaces. The authors show that DNNs achieve optimal minimax rates and match upper and lower bounds on learning error, something not established in previous works. The theoretical results are supported by evaluations on challenging problems such as Navier-Stokes-Brinkman Equations (NSB) and Boussinesq PDEs.

🧩 Key Contributions

• The paper constructs a class of DNNs that show that for any approximate minimizer, the error between the true $F$ and $\hat{F}$ is bounded above. The error defined is decomposed into approximation error, decoding-encoding errors, and how well the encoder-decoder pairs approximate the identity maps on $X$ and $Y$ respectively. The approximation error in particular decays algebraically with the amount of training data $m$. The theorem that demonstrates this focuses primarily on tanh functions.

• The paper continues with a lower bound and shows that regardless of method, one cannot do better than the product of some constant $c(p)$ and exponent $\alpha$, or $c(p)m^{-\alpha}$ where $\alpha = 1 - \frac{1}{p} - \frac{1}{q}$.

• The authors present numerical results applied to different parametric PDE problems (parametric elliptic diffusion equation, Navier-Stokes-Brinkman equation, and the parametric stationary Boussinesq equation) to further demonstrate their theoretical framework.

✅ Strengths

• Although this paper is outside my comfort zone, I understand the novelty and appreciate the theoretical rigor in evaluting the optimality of using DNNs for operator learning. That sort of rigor is sorely lacking in modern research.

• The paper's rigor in establishing matching upper and lower bounds and covering the more general Banach spaces (as opposed to Hilbert spaces like the bulk of other literature does) is pretty impressive.

⚠️ Weaknesses / Questions

• I do wish there was a little more meat when talking about "classical" ways of operator learning, at least outside of the author's prior works. I'm more interested in seeing those more classical methods so it can connect nicely into why I care about this DNN versus one of those methods.

• One example is using Fourier series to approximate the smooth functions over a domain which is known to suffer from curse of dimensionality and can quickly become intractable at higher dimensions. This DNN apparently avoids that same curse of dimensionality.

• In the slide presentation, literally all 5 references are the author's own works without any external references. Further, this work is fairly self-referential. However, there is a distinct lack of rigorous research into this era, so it's totally possible this author is one of the few in the world working in this problem space.

🔍 Appendix A: Example

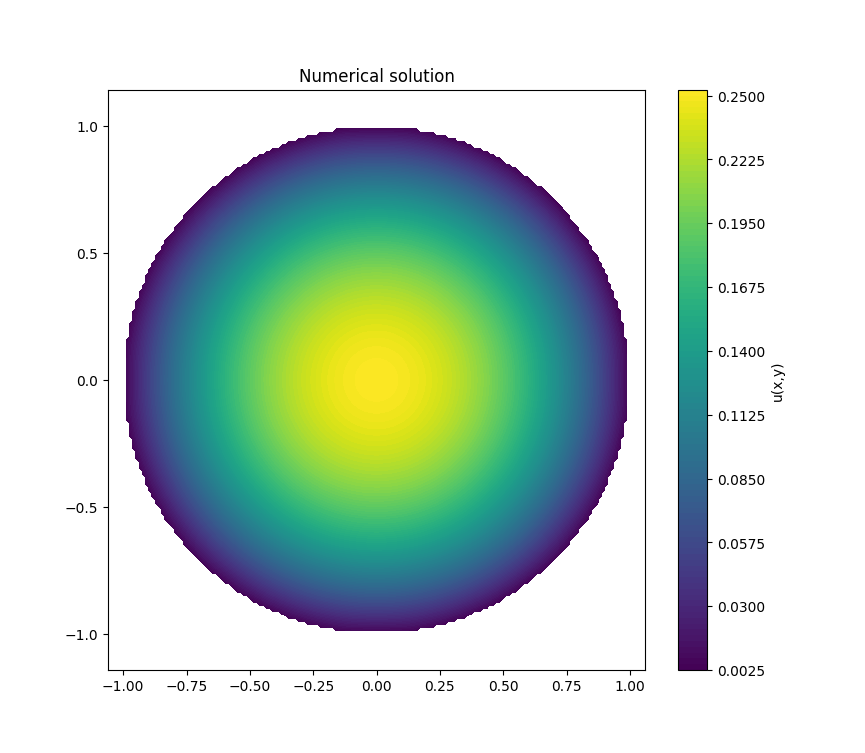
To refresh myself in this domain and better understand this paper, I attempted to build a simple sample problem below.

Example Domain (Open Unit Disk):

$$\Omega = \bigl\{\, (x,y)\in\mathbb{R}^2 \bigl| x^{2}+y^{2}<1 \,\bigr\}$$

Equation over the domain (One-component reaction-diffusion equation). Note that g(x,y) is added as a forcing term to the RHS:

$$- \Delta u(x,y) + \lambda \, e^{u(x,y)} = g(x,y), \quad \text{for } (x,y) \in \Omega$$

Equation with added Dirichlet Boundary Condition ($u(x,y)=0$) on the boundary of the open unit disk):

$$\begin{cases} - \Delta u(x,y) + \lambda \, e^{u(x,y)} = g(x,y), & \text{for } (x,y) \in \Omega, \\ u(x,y) = 0, & \text{for } (x,y) \in \partial\Omega. \end{cases}$$

where $\Delta u = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}$ (the Laplacian operator), and $\lambda$ is the scaling parameter ($\lambda = 1$ is fine).

We pick $u^* = \frac{1}{4}(1 - x^2 - x^2)$ as a solution which satisfies the boundary condition defined above, and then we can solve for $g(x,y)$ (the external term):

$$u^*(x,y) = \frac{1}{4}(1 - x^2 - y^2)$$

and we compute the Laplacian:

$$\Delta u^* = \frac{\partial^2 u^*}{\partial x^2} + \frac{\partial^2 u^*}{\partial y^2} = (-\frac{1}{2}) + (-\frac{1}{2}) = -1$$

and hence the forcing term becomes:

$$g(x,y) = -\Delta u^* + \lambda e^{u^*} = 1 + \lambda e^{\frac{1}{4}(1 - x^2 - y^2)}$$

We can then solve the following non-linear equation $F(u)$ using Newton's method.

$$F(u) = -\Delta u + \lambda e^{u} - g = 0$$ $$F(u(x,y)) = -\Delta u(x,y) + \lambda \left[ e^{u(x,y)} - e^{\frac{1}{4}(1 - x^2 - y^2)} \right] - 1$$

Note that unlike the paper, my domain is over $\mathbb{R}$, not $\mathbb{C}$, so the operator $F$ is not holomorphic. However, it still acts between two real Banach spaces. Solving using a mesh size of 320 provides a nice visualization below, and an error of $1.966e-3$.

🔍 Related Work

• Functional Analysis

• Operator and Function approximation

📄 Attachments

PDF

📄 View PDF

Slides

🎤 View Slides

Code

🧑‍💻 GitHub Repository

Paper Link

🔗 External Page